In my work as a data scientist at Project A. I often encounter the task of predicting customer behavior. For many businesses it can be very valuable to estimate which one of their new customers will be the most profitable in the future. Or which one of the existing customers will stop being valuable. In this context many tasks such as predicting churn, customer lifetime value or ending of newsletter subscription are of interest. While these tasks sound very different the principles can be easily generalized to any predictive modeling task. Here, I will evaluate on the general principle.
Time scale
Usually, it is not of interest to predict any arbitrary time point in the future. It is sufficient to estimate the target variable of interest for a specific point in time, e.g. the behavior of a customer in 12 months from now. This makes the modeling of our problem a lot easier. Instead of forecasting a complex time series we only need to make a single point estimate.
To formalize this a little bit. We want to predict the customer behavior in $t$ months from now. And denote the customer behavior as $y_t$ and our prediction with $\hat{y_t}$. We do this prediction based on our current observations of the customer $x_0$ (e.g. his buying frequency, his created revenue up to date) .
Data
Data is the key component in predictive modeling. We want to make a prediction of the future based on our observations in the past. So in order to train a predictive model that predicts how customers behave in $t$ months from now. We actually go $t$ months in to the past look at our observation $x_{-t}$ and build a model $m_{now}$ that predicts our current customer behavior $y_{now}$
$$
\underset{m_{now}}{\mathrm{argmin}} (\hat{y}_{now} - y_{now})
\underset{m_{now}}{\mathrm{argmin}} (f(x_{-t},m_{now}) - y_{now}).
$$
We do also add a regularization term $R(f)$ as our aim is not learning the training data perfectly but to generalize as good as possible
$$
\underset{m_{now}}{\mathrm{argmin}} \bigg(\Big(f(x_{-t},m_{now}) - y_{now}\Big) - \lambda \Big(R(f)\Big)\bigg).
$$
Validation
The classical way of validating machine learning models is cross validation. For cross validation we estimate or train our model on a subset of the data. And estimate its performance on the remaining set. We can do this multiple time so that each customer was at some point part of the training dataset and at some point part of the testing dataset. This is good because it tells us how well we generalize towards new customers.
However, here we are not so much interested in how well our predictive model generalizes to new customers. Rather we are interested how well our model generalizes over time. Therefore we might want to validate our approach by learning a model $m_{-t}$ that trains on observation data $x_{-2t}$: $$ \underset{m_{-t}}{\mathrm{argmin}} \bigg(\Big(f(x_{-2t},m_{-t}) - y_{-t}\Big) - \lambda \Big(R(f)\Big)\bigg). $$ This model is ideal to validate the temporal generalization of our approach. We can apply it onto our observation at time point $-t$ to predict our current observation: $$ f(x_{-t},m_{-t}) = \hat{y}_{now} . $$ The difference between our prediction and the actual customer behavior: $$ {y}_{now} - \hat{y}_{now} , $$ can be a good estimate how our approach generalizes over time.
Another valid approach is store your predictions and to monitor their development and ideally their convergence over time.
Communication and Alignment
A problem which is a lot of times underestimated is intense communication with the stakeholders. Often additional hours spend in the initial alignment phase can save days in later phases. Here, I recommend to ask stakeholders how they want to use the result of the predictive model. Sometimes, you will find out that a simple statistic is sufficient or the problem is very different to how it was initially described. Additionally, I recommend to mutually align on points and iterate until everyone is on the same page.
Methods
On the contrary a problem which is often over estimated is the choice of a machine learning method. Often people want to work a like to machine learning method papers and compare 5 to 10 different methods. While a new machine learning method has to be compared to others to give evidence for its relevance the value in creating a new data product is rather small. Usually spending time in feature engineering or acquiring more labeled data is much better spend. Here is an Illustration by Banko and Brill showing impressively that data is more powerful than algorithms:
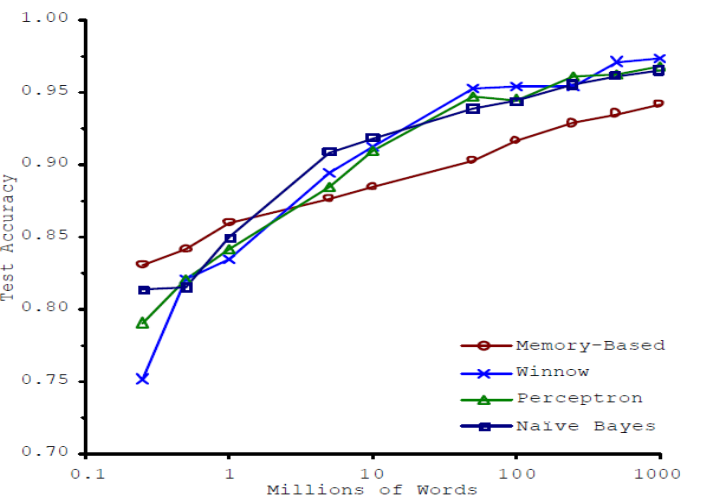
It is claimed that more modern approaches like deep learning are mainly performing better because they able to encode more data. This also points to algorithmic complexity and the question how well an algorithms scales with data.
